Wie Berechnet Man Den Flächeninhalt Eines Kreises Mit Dem Durchmesser

Du sollst Durchmesser, Umfang und Fläche von einem Kreis berechnen? Das ist einfacher als du denkst. Wir zeigen dir, welche Formeln du anwenden musst und wie die Rechenwege aussehen. Stelle anschließend dein Wissen auf die Probe und löse unsere Übungsaufgaben!

Der Kreis ist eine perfekt runde geometrische Form. Jeder Punkt des Kreises hat den gleichen Abstand zum Mittelpunkt. Das unterscheidet einen Kreis zum Beispiel von einer Ellipse.

Der Kreismittelpunkt M liegt genau in der Mitte des Kreises.

Kreis berechnen – Alle Formeln, dice du brauchst!

Fläche: A = π · r² oder A = π · d² · ¼

Umfang: U= 2 · π · r oder U = π · d

Radius Kreis

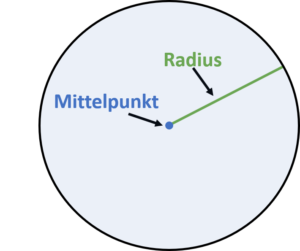
Du möchtest einen Kreis berechnen? Wenn du den Radius kennst, ist das ganz einfach!

Der Radius eines Kreises ist der Abstand vom Kreisrand (auch Kreislinie genannt) zum Mittelpunkt.

Zeichnest du einen Kreis mit dem Zirkel, stellst du bei ihm vorab den Radius ein.

Durchmesser Kreis

Der Durchmesser d eines Kreises ist der Abstand von einem Punkt auf der Kreislinie zu dem Punkt auf der gegenüberliegenden Seite.

Dabei verläuft die Gerade durch den Mittelpunkt. Einfacher ist dies optisch darstellbar:

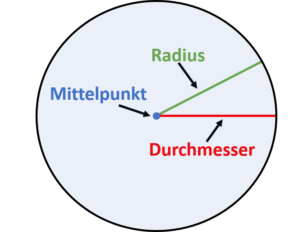
Wie du siehst, ist der Durchmesser doppelt so lang wie der Radius. Daher gilt:

Durchmesser: Übung

Du hast einen Kreis mit einem Durchmesser von 7,v cm. Wie groß ist der Radius des Kreises?

Lösung

Wir haben den Radius des Kreises vorliegen:  r = seven,5 cm. Diesen Wert setzen wir in die Formel ein:

r = ½ · d
r = ½ · 7,five cm
r = 3,75 cm

Der Radius des Kreises beträgt 3,75 cm.

Umfang Kreis

Der Umfang U eines Kreises ist die Länge der Kreislinie. Stell dir vor, du würdest den Kreis abrollen und dice Strecke messen. Ihre Länge entspricht dem Umfang. Für die Berechnung des Umfangs eines Kreises benötigst du den Radius oder den Durchmesser und dice Kreiszahl Pi:

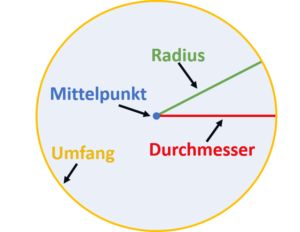
U = Umfangπ = Kreiszahl Pi ≈ 3,xivd = Durchmesser  r = Radius

Beispiel: Umfang Kreis berechnen

Ein Kreis besitzt einen Radius von 11 dm. Wie groß ist der Umfang?

Gegeben: r = 11 dm

→ Dies setzten wir in die oben genannte Formel ein:

U= 2 · π · r
U = ii · π · eleven dm
U = 22 dm · π
U ≈ 69,12 dm

Der Umfang des Kreises beträgt ca. 69,12 dm. Beachte auch immer die Angabe der richtigen Maßeinheit (hier: Dezimeter)!

Und nun bist du an der Reihe! Teste mit den folgenden Übungsaufgaben, ob du dice Anwendung der Umfangformel verstanden hast.

Umfang: Übung 1

Berechne den Umfang eines Kreises mit dem Radius r = three cm.

Lösung

Du weißt den Radius des Kreises (r = 3 cm). Diesen kannst du in einfach in die Fomel einsetzen:

Umfang Kreis berechnen: U = ii · π · r

U = ii · π · r
U= ii · π · 3 cm
U ≈ 18,85 cm

Der Umfang des Kreise beträgt ca. eighteen,85 cm.

Umfang: Übung 2

Berechne den Umfang eines Kreises mit Durchmesser d = ten cm.

Lösung

U = π · d
U = π · 10 cm
U ≈ 31,416 cm

Der Umfang des Kreises beträgt ca. 31,42 cm.

Fläche Kreis

Der Flächeninhalt A eines Kreises ist dice Größe der Kreisfläche.

Auch für die Berechnung der Kreisfläche brauchst du Radius (bzw. Durchmesser) und die Kreiszahl Pi.

A = π · r²
A = (π · d²)/4

A = Fläche des Kreisesπ= Kreiszahl Pi ≈ 3,14d = Durchmesserr = Radius

Beispiel: Kreisfläche berechnen

Ein Kreis besitzt einen Radius von four,v cm. Wie groß ist der Flächeninhalt?

Gegeben: r= four,v cm → d = 9 cm

→ Dies setzten wir in die Formel ein:

A = (π · d²)/four
A = (π · 9²)/four
A = (π · 81)/4
A ≈ 63,62 cm²

Der Flächeninhalt des Kreises beträgt ca. 63,62 cm². Achte darauf, dass bei Flächeninhalten das Ergebnis im Quadrat (hier: cm²) stehen muss!

Konntest du die Anwendung der Flächenformeln nachvollziehen? Teste es in den zwei folgenden Übungen!

Fläche: Übung 1

Ein Kreis chapeau einen Radius von r = 7 cm. Berechne die Kreisfläche.

Lösung

Fläche Kreis berechnen:

A = π · r²
A = π · (7 cm)²
A = π · 49 cm²
A ≈ 153,94 cm²

Der Kreis hat einen Flächeninhalt von ca. 153,94 cm².

Fläche: Übung 2

Berechne den Flächeninhalt eines Kreises mit dem Durchmesser d = 21 mm. Wandle das Ergebnis in Quadratzentimer um.

Lösung

A = (π · d²)/four
A = (π · (21 mm)²)/four
A = (π · 441 mm²)/4
A ≈ 346,36 mm²

346,36 mm² ≈ 3,46 cm²

Dice Fläche des Kreises beträgt gerundet ca. 3,46 cm².

Ein alternativer Lösungweg wäre, den Durchmesser  vorab in r umzuwandeln (r = ½ · 21 mm = 10,5 mm) und in die Formel A = π · r² einzusetzen.

Tipp: Überlege dir selbst Beispielaufgaben, um dice Kreisformeln zu üben. Auf der Seite Rechneronline kannst du im Anschluss nachschauen, ob du dice richtige Lösung hast.

FAQ

Zum Abschluss haben wir eure häufigsten Fragen zum Kreis haben hier gesammelt. Klicke einfach auf das +, um die Antwort lesen zu können.

Was ist ein Kreis?

Ein Kreis ist eine geometrische Figur, bei der alle Punkte der Kreislinie den gleichen Abstand zum Mittelpunkt haben.

Was bedeutet r im Kreis?

Das Kürzel r steht für den Radius des Kreises. Der Radius ist der Abstand von der Kreislinie zum Kreismittelpunkt.

Wie viel Grad chapeau ein Kreis?

Ein Vollkreis chapeau 360 Grad.

Warum chapeau ein Kreis 360 Grad?

Teilst du den Kreisbogen in 360 Stücke, wird der Abstand zwischen zwei Stücken als "1 Grad" bezeichnet.

Dies lid historische Gründe. Die Einteilung geht vermutlich auf die Babylonier zurück, die vor 4000 Jahren ein Zahlensystem entwickelten, das von sixty ausgeht. Dieses 60er-System ist auch bei uns noch im Gebrauch – and then hat etwa eine Minute 60 Sekunden und eine Stunde 60 Minuten.

Wie viele Symmetrieachsen chapeau ein Kreis?

Ein Kreis lid unendlich viele Symmetrieachsen.

Ich hoffe der Artikel war hilfreich und wir haben uns nicht zu sehr im Kreis gedreht. 😉

Für Fragen und Anregungen stehen wir gerne zur Verfügung und sind froh, wenn wir euch helfen können!

Falls du uns noch ein Kommentar mit deiner Meinung oder eine Sternebewertung hinterlassen möchtest, würden wir uns sehr freuen!

iv,32 von five Sterne Loading...

Source: https://www.nachhilfe-team.net/lernen-leicht-gemacht/kreis-berechnen/

Share this post